Wizards' Handbook by Dictum Mortuum (3.5e Optimized Character Build)/Spells

Save-Based Spells

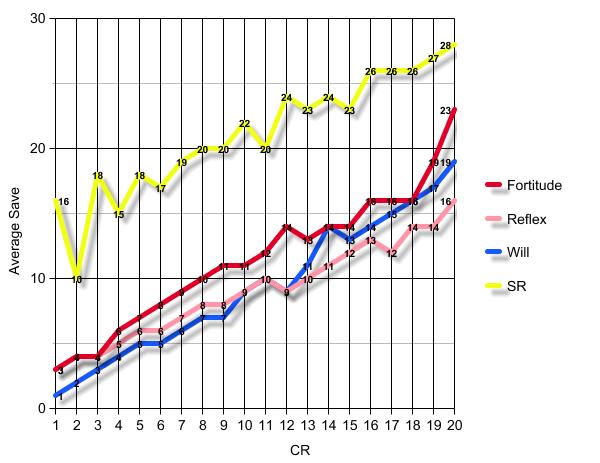
Unless you are a fairly experienced player you will probably have a problem selecting the right spells at each level. There are spells that deal with specific creature types, but what if someone wants to be prepared no matter what? What spells should he memorize for the day when he reaches a certain level? Even worse what saving throws should his spells allow? A way to cover this problem is to consult the graph below:

This actually presents the creatures' (of a certain challenge rating) average scores (in saves and SR). Data come from CubeKnight's creature filter and as you can see there are records from lots of different source books.

Fortitude saves are almost always the best saving throws. Even though after mid levels they sometimes are equal to will saves, they never fall below that limit. On the other hand, will saves are the worst saves at early levels, but they get significantly boosted at mid and late levels. Reflex saves are probably the worst saves there are. At low levels they are better than fortitude saves, but at mid and higher levels will saves are superior. Reflex saves are significantly lesser at high levels, not the difference between fortitude (23 on average) and reflex (16 on average).

So to wrap it up:

• Low to Mid Levels (1-10 CR):
  • Fortitude > Will
  • Fortitude >= Reflex
  • Reflex >= Will

• Mid to High Levels (11-20 CR):
  • Fortitude >= Will
  • Fortitude >> Reflex
  • Reflex <= Will

So now selecting your spells should be relatively easier. If you study the graph, from low to mid levels your will-based spells are less likely to be resisted. The same goes for reflex-based spells and high levels. Mind you, i am not suggesting that fortitude-based spells are bad, just that they are less likely to be effective (that is actually correct, since most save or die spells fall into this category).

Difficulty Class

Simply put, for your spell to be effective you want your opponent to score on his d20 saving throw check a number less than your DC minus his save bonus:

1d20 check < Your DC - His Save

For example, a 1st level wizard with 18 intelligence casts sleep. Thus, his difficulty class is 15 (10 + spell level + int modifier). His target is a 1st level fighter with a fortitude saving throw of 5 (2 base + 3 con modifier). Using the above formula we have: 1d20 check < 15 (DC) - 5 (Save) = 10. So for the wizard's spell to be effective, the fighter must score a number between 1 and 9. Since a 20 is a critical success however, this is too, factored in. Now what is the chances of the spell to land? We have nine numbers between 1 and 9. That's 9 times out of 20, so the chances that the spell succeeds are 45%. The best chance you will ever get is 95% for your spell to be effective. That's because a natural 20 is always a success. To raise the effectiveness of your spells, you can either a) reduce your opponent's saving throw b) increase your save DC. That said, pumping *up your intelligence isn't always the optimal way to go, but the mainstream one. There are lots of effects that reduce your opponents' saving throws, cheap and efficiently.

Now assume a wizard with 18 intelligence in a party of 4. Let's see what his chances are when facing creatures of a challenge rating equal to his party members' average level. Note that we assume that he is using his best spell available (see bottom of section, "Early/Mid chances for spells").

After studying the results, we come to the following conclusions:

• If the result of DC - Save is less than or equal to 0, you always fail to affect your target, except for a critical miss. Results in 5% chance of success.
• If the result of DC - Save is higher than or equal to 20, you can only lose to a natural 20. That gives you a 95% chance of success.
• If the result is 0 < DC - Save < 20, then your chance of success is calculated by dividing the result by 20 and multiplying by 100 %. For example i have a result of 10. That divided by 20 results in 0,5. We now multiply it by 100% and get: 50% chance of success.
• Of course, all wizards should try to maximize their DCs to their full potential. That means the biggest chance of success, 95%. **Every point of penalty you apply to your opponents' saves results in a 5% raise in your chance of success, but it is capped at 95%. **Every point of bonus DC you get, again, is a 5% raise to your chance, with the same limitation.

If we use again the iconic 18 starting intelligence wizard, his intelligence is going to be (after using tomes and powerful magic items): 18 (starting) + 5 (tome) +5 (levels) +6 (headband of intellect) = 34. This is a +12 modifier, meaning that your DC for x level spells is: 12 + x. Assuming a y saving throw bonus we have:

1d20 < 12 + x - y

As you can see above, to reach the maximum chance of success, we need to have:

12 + x - y >= 20 =>x - y >= 8

Remember that x is the level of the spell. Spell levels belong to: [1, 9]. So we have: D = { (x,y) belong to Z : 1 <= x <= 9 and y <= 8-x }. If a pair of (x,y) fulfills this requirement, then you'll have maximum chance of success with a starting intelligence of 18 and all the normal benefits you can acquire (items, not including classes and racial mods). Seems pretty limited, since if we use a 1st level spell for example (x=1) then your opponent's saving throw bonus can't be greater than 1 (y<=1).

Early/Mid chances for spells

• CR 1
  • Fort: 60%
  • Reflex: 70%
  • Will: 70%

• CR 3

• • Fort: 60%
  • Reflex: 65%
  • Will: 65%

• CR 5
  • Fort: 50%
  • Reflex: 55%
  • Will: 60%

• CR 7
  • Fort: 45%
  • Reflex: 55%
  • Will: 60%

• CR 9
  • Fort: 40%
  • Reflex: 55%
  • Will: 60%

Spell Resistance

Enter spell resistance. Many creatures possess this ability and can prove quite the nuisance, since a creature will be protected even more by your spells. The main formula is:

1d20 >= His SR - Your CL

As you can see now you are making the check, so the higher you score, the better. To calculate your chance of success, calculate: 21 + your CL - his SR. Divide the result by 20 and multiply it by 100%, and you have your chance of success.

e.g. A wizard with caster level 10 targets a SR 19 opponent. 21 - 10 + 19 = 12. 12/20 * 100% = 60%. So the wizard's chance of success will be 60%. Which actually means that if you score anything greater than or equal to a 9, you succeed.

A tricky part worth noting is: what if a spell requires both SR and saving throw check? What are my chances of success then? Well simply multiply the success chances between them and you'll have the new one.

e.g. A wizard with CL 10 and intelligence 18 targets an SR 19 and 1 saving throw bonus opponent. What is his chance of 1st level spell that requires both checks to succeed?

• Saving throw part chances: 15 - 1 = 14. That is the equivalent of a 70% chance of success.
• Spell Resistance part chances: 21 - 19 + 10 = 12. That's 60% chance of success.

Final calculation: (60/100)*(70/100) = (4200/10000) = (42/100) = 42% chance of success.

Even though the numbers will vary, this is an example of high chance rolls. When you have to make both checks however, as you can see, the chances to succeed are a lot less.

Touch Attacks

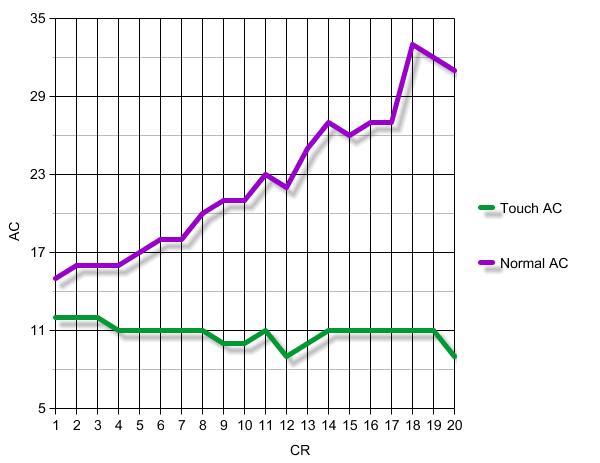
There are spells that require ranged or melee touch attacks to hit their targets. Failure to do so means your spell is lost. Let's study the touch attacks by challenge rating chart:

As you can see, touch ACs are high in low challenge ratings and they gradually fall even more. This is not the case with normal AC ratings, which are constantly rising. We assume a wizard with no other bonuses to his attack roll than his BAB. Wizards have bad BAB progression, but since touch AC scores get worse as you will be gaining levels, it will be easier for you to get touch spells through. So at first level they get a 45% chance of success, while at twentieth level you get a 95% chance.

To calculate the chances of your success, use the following formula:

1d20 >= His Touch AC - Your Attack Bonus

Calculate 21- (AC - attack bonus) and divide that by 20. Multiply by 100% and then you get your chances.

Again, as with spell resistance, there are spells that require both a touch attack and a spell resistance check. There are even those who require all three of these rolls. To calculate your overall success, multiply all your separate chances together.

For example, you have a 50% chance of beating SR and a 60% of beating touch AC. Your opponent has a 40% chance of saving against your spell. That means that you get: (50/100)*(60/100)*(40/100) = (50*40*60/1000000) = 12% barely.

A special note, even if you got 95% separate chances of success (which is the higher chance you will ever get) for each roll, you get: (95/100)*(95/100)*(95/100) ~= 85,7%. That said, spells that require many rolls to succeed are naturally inferior to those that require just one. So to maximize your chances of success you don't only need high DCs for spells, but spells with a small number of required rolls, too.

Concentration Checks

Concentration is a skill that generally wizards need to max out and this is because many effects linked to spells require concentration checks. Should you fail to concentrate on your spell, you are most likely going to lose it. The player's handbook provides detailed information on page 170 on concentration checks, that will cover almost all cases. Most notably:

• Injury while casting a spell: In case of continuous damage, you should be able to succeed. The problem here is if damaged by attacks or, even worse, enemy spells. Since opponents can ready an action to "when the enemy starts casting a spell", they will be able to affect even those spells that require a standard or move action to cast. Miss chance, invisibility and damage reduction can help lessen the inflicted damage, thus making your concentration check easier.
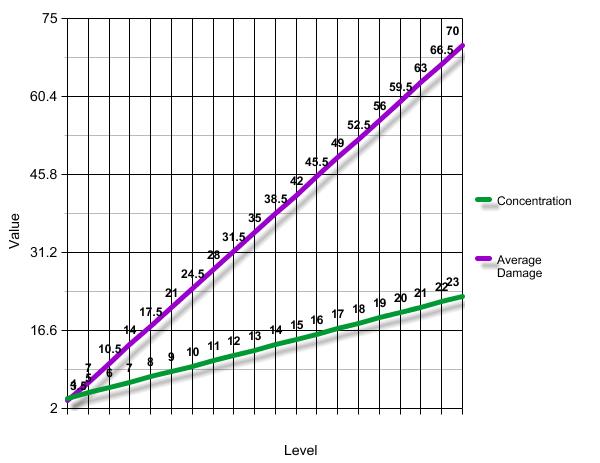
• Distraction by spell: Mundane attacks only get 1/2 of the inflicted damage dealt to the concentration check's DC. Note that this is not the case with spells that deal damage. They actually add all the inflicted damage to the check. Thus, even a lowly magic missile PHB spell (which if of 9th and higher caster level has a damage of 10-25, resulting in an average damage of 17,5) will boost your concentration check to 27,5 + level of the spell you're casting, nothing to scoff at.

This graph shows how the damage of a spell, which deals 1d6 points of damage per caster level, scales compared to your concentration check with no modifiers.

---

Back to Main Page → 3.5e Homebrew → Optimized Character Builds → Wizards' Handbook by Dictum Mortuum